Clase 21 de diciembre de 2015 EXAMEN

Querido diario:

el día 21 tuvimos un examen de trigonometría por parejas,yo lo hice con Iciar, utilizando herramientas como Wiris y GeoGebra, así que aquí dejo resueltos todos los ejercicios que nos planteó el profesor.

1.- Definición de incentro de un triángulo. Calcula, paso a paso, utilizando WIRIS, el área de la región plana comprendida entre la circunferencia inscrita y la circunferencia circunscrita al triángulo isósceles cuyos lados iguales miden 3 unidades y el ángulo comprendido entre dichos lados mide 0’5 radianes. ¿Dicha región es una corona circular? Razona tu respuesta. Dibuja dicha región utilizando GEOGEBRA y PAINT. Guarda en tu carpeta de trabajo los correspondientes archivos.

Incentro: punto de corte de las bisectrices de dos ángulos interiores cualesquiera de dicho ángulo. La bisectriz del tercer ángulo interior pasa por el incentro.

SOLUCIÓN GRÁFICA GEOGEBRA

 La región no es una corona circular porque los centros de ambas circunferencias no coinciden.

2.- Se quiere reconstruir la ubicación y las dimensiones de un claustro de forma cuadrada desaparecido y del que se ha encontrado su pozo. Se tienen dudas de la ubicación del pozo en relación al claustro pero se sabe que dicho pozo distaba 30, 40 y 50 m de las esquinas del claustro. Utiliza WIRIS para realizar los cálculos paso a paso y dibuja la solución con GEOGEBRA. Guarda en tu carpeta de trabajo los correspondientes archivos.

 

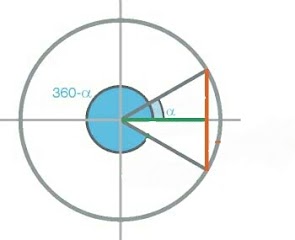
SOLUCIÓN GRÁFICA GEOGEBRA

3. Una barra de longitud constante AB se desliza sobre una semicircunferencia, de modo que sus extremos A y B están siempre sobre la semicircunferencia. En cada posición de la barra proyectamos los extremos de la misma sobre el diámetro de la semicircunferencia y construimos el triángulo de vértices MPR , siendo M el punto medio de la barra. ¿Cómo evolucionará el triángulo?

a)      Elabora una construcción dinámica con GEOGEBRA que permita ver dicha evolución.

b)      Demuestra, utilizando el teorema de Tales, que el triángulo MPR es isósceles.

c)      Como el segmento AB se desliza por la semicircunferencia, el triángulo MPR varía, demuestra que cualquiera de esos triángulos MPR son semejantes.

Guarda en tu carpeta de trabajo los correspondientes archivos.

A.

B. 

C. Son semejantes porque si aumento la altura, la base disminuye y si la base aumenta, la altura disminuye.

4.- Resuelve el triángulo DEN sabiendo que ABCDE es un pentágono regular, M es el punto medio del radio, en el eje OX, de la circunferencia circunscrita a dicho pentágono y que tomamos como unidad de medida, N es un punto en el eje OX tal que DM = NM. Utiliza WIRIS para realizar los cálculos paso a paso y dibuja la figura con la solución utilizando GEOGEBRA. Guarda en tu carpeta de trabajo los correspondientes archivos.

Clase 18 de diciembre de 2015

Querido diario:

aquí os dejo un artículo realmente interesante que nos ha enviado nuestro profesor.

http://naukas.com/2013/05/22/por-que-se-sincronizan-los-metronomos/

En él habla sobre cómo una serie de metrónomos que no están sincronizados situados sobre una superficie móvil al cabo de un tiempo acaban sincrónizandose!! Es algo realmente curioso que al leerlo me hizo pensar en lo importante que es para nosotros en entorno en el que estamos y aquellos que se encuentran en él. La mayoría de las personas acaban haciendo lo que los demás hacen y finalmente todos parecemos clones, así que deberíamos plantearnos ¿en qué me diferencio con los demás? ¿soy capaz de saber decir no cuando estoy bajo la presión de grupo? Esto segundo puede ser determinante en nuestras vidas y es algo que tenemos que tener claro, hay que saber decidir qué es lo que YO quiero hacer, ya que tendrá una serie de consecuencias que tendremos que afrontar, pero así sabremos que fue una decisión propia y no de otra persona a la que imité. 

Clase 18 de diciembre de 2015

Querido diario:
ya llegamos al final de tema, como ya hemos visto las ecuaciones trigonométricas hoy veremos cómo resolver los SISTEMAS DE ECUACIONES TRIGONOMÉTRICAS.

Sistemas que se pueden resolver por reducción

Reducibles a ecuaciones algebraicas

Reducibles mediante relaciones trigonométricas

Clase 15 de diciembre de 2015

Querido diario:
continuemos con este tema...hoy comenzaremos con TRANSFORMACIONES DE SUMAS DE DOS RAZONES EN PRODUCTOS.

Transformación de la suma /de la diferencia de senos en productos

Transformación de la suma / de la diferencia de dos cosenos en producto

Ejemplo:

ECUACIONES TRIGONOMÉTRICAS

Ecuaciones del tipo una función trigonométrica igualada a una constante

Ecuaciones que hay que factorizar

Ecuaciones en las que hay que expresar todas las razones trigonometricas en función de una sola

Clase 14 de diciembre de 2015

Querido diario:
hoy comenzamos un nuevo tema, que no es más que la segunda parte de la trigomometría!

RAZONES TRIGONOMÉTRICAS DE LA SUMA / DIFERENCIA DE DOS ÁNGULOS

- Seno de la suma/de la diferencia de dos ángulos

- Coseno de la suma/ de la diferencia de dos ángulos

- Tangente de la suma / diferencia de dos ángulos

RAZONES TRIGONOMÉTRICAS DEL ÁNGULO DOBLE

A partir de las razones trigonometricas de la suma de dos ángulos obtenemos las siguientes:

RAZONES TRIGONOMÉTRICAS DEL ÁNGULO MITAD

   Seno

 Coseno

 Tangente

Ejemplo:

Ejercicios tema 4 trigomometría

Querido diario:
aquí iré dejando los ejercicios resueltos del tema.

EJERCICIO 1 
Responde a las siguientes cuestiones:
A. Expresa en radianes
B. Pasa a sexagesimales
C. Dados ciertos ángulos realiza las operaciones indicadas

EJERCICIO 2
Resuelve los siguientes triángulos.

EJERCICIO 3
De un triángulo rectángulo sabemos que uno de los catetos es el doble del otro. Halla los ángulos del triángulo. Si además se conoce que su hipotenusa mide 3m, halla las longitudes de los catetos.

EJERCICIO 4
Desde un cierto punto del suelo se ve un árbol bajo un ángulo de 50° ¿Bajo qué ángulo se verá colocándose a distancia doble? ¿Y a distancia triple?

EJERCICIO 5
Un paseante se dirige hacia un castillo. Desde una torre de 75 m se ve al paseante bajo un ángulo de 64° con la vertical y un minuto después el ángulo de visión se reduce a 3w°¿Qué velocidad en km/h lleva el caminante?

EJERCICIO 10
Halla las razones trigonometricas sabiendo que el seno es -7/12 sabiendo que está en el tercer cuadrante.

Clase 11 de diciembre de 2015

Querido diario:
seguimos hablando de la trigonometría...hoy en concreto sobre LAS EXPRESIONES DEL ÁREA DE UN TRIÁNGULO.
Como sabemos desde pequeños el área de un triángulo es (base * altura)/2 , pero podemos obtener otras fórmulas usando la trigonometría.

Fórmula de Herón
Pretendía que el área dependiese de los 3 lados.

Demostración:

Clase 10 de diciembre de 2015

Querido diario:
hoy voy a contar CÓMO SE RESUELVE UN TRIÁNGULO CUALQUIERA. Recordemos que resolver un triángulo es obtener los 3 lados y 3 ángulos.
- Si conozco los 3 lados
Debemos tener en cuenta la siguiente proposición:

Resuelve el siguiente triángulo

Podemos comprobar la proposición anterior con este ejemplo 4-2 < 5 < 4+2

Para resolver el triángulo utilizaremos el teorema del coseno.

 

*Se podría haber resuelto también mediante el teorema del seno una vez obtenido el primer ángulo, y para obtener el último mediante la diferencia(suma de todos sus ángulos es 180), es una forma más rápida pero he querido hacerlos todos igual para trabajar el teorema del coseno.

-Si conozco un lado y los ángulos de sus extremos

Para resolverlo debemos tener en cuenta que la suma de todos sus ángulos es 180°, después utilizaremos el teorema del seno para conocer los lados restantes.

-Si conozco dos lados y el ángulo comprendido entre ellos

Calcularemos el lado que nos falta mediante el teorema del coseno y los ángulos restantes mediante el teorema del seno.

- Si conozco los dos lados y en ángulo opuesto a uno de ellos

Calculamos uno de los ángulos mediante el teorema del seno, y el otro sabiendo que todos suman 180°. Para el lado que falta se vuelve a aplicar el teorema del seno.

Reflexión primera evaluación

Querido diario:

después de los primeros meses de curso toca ponerse a pensar en el trabajo realizado...¿realmente merezco la nota que tengo? ¿he trabajado lo suficiente? ¿este es el máximo esfuerzo que puedo hacer? ¿qué debo mejorar?

Bien, la primera evaluación suele ser más complicada, es inicio de curso y además no conoces al profesor, y he de decir que me ha sorprendido su forma de hacernos trabajar, mismamente con este blog, pero creo que aunque sea algo costoso, cuando subo entradas estoy asimilando día a día aquello que damos en clase. 

Creo que he trabajado bastante en esta evaluación pero claramente no lo he hecho todo, y para mejorar en mi proceso de aprendizaje me propongo hacer algo que me ha faltado esta evaluación...hacer todos los ejercicios del libro! Creo que me puede ayudar a reforzar los contenidos y ya he visto cómo evoluciona la asignatura y cómo organizarme. 

El trabajo en equipo me ha ayudado mucho porque he entendido cosas que antes no conseguía hacer y he visto cómo trabajan otras personas y he podido aprovecharme, en el buen sentido de la palabra, de cada uno de los componentes de mi grupo para mejorar personalmente en mi forma de trabajar. Eso sí! Fuera comparaciones! Que me apoye en otras personas no quiere decir que tenga que compararme con ellas, cada uno es como es.

¡Espero seguir aprendiendo poco a poco en esta evaluación que viene y mejorar este blog! Aún queda mucho por hacer. 

 

Clase 4 de diciembre de 2015 (II)

Querido diario:
hoy os voy a hablar sobre algunos presonajes destacados en el mundo de la trigomometría.

HIPARCO DE NICEA
Hiparco de Nicea, también conocido como Hiparco de Rodas, fue un matemático y astrónomo griego, el más importante de su época.
Hiparco nació en Nicea, Bitinia (hoy Iznik, Turquía), alrededor del año 190 a.C

Realizó importantes contribuciones a la trigonometría tanto plana como esférica, publicó la tabla de cuerdas, temprano ejemplo de una tabla trigonométrica, cuyo propósito era proporcionar un método para resolver triángulos. También introdujo en Grecia la división del círculo en 360 grados.
En astronomía descubrió la presesión de los equinoccios y describió el movimiento aparente de las estrellas fijas cuya medición fue de 46', muy aproximado al actual de 50,26". Calculó un periodo de eclipses de 126.007 días y una hora.
Hiparco también calculó la distancia a la Luna basándose en la observación de un eclipse el 14 de marzo de 190 a.C. Su cálculo fue entre 59 y 67 radios terrestres, el cual está muy cerca del real (60 radios). Desarrolló un modelo teórico del movimiento de la luna basado en epiciclos.

CLAUDIO PTOLOMEO DE ALEJANDRÍA

Claudio Ptolomeo, astrónomo, matemático y geógrafo egipcio del siglo II de la era cristiana, nace en Tolemaida Hermia, en el Alto Egipto, alrededor del año 100, y vive y trabaja en Alejandría.

Para su uso como astrónomo inventó una trigonometría, tan completa, que sobrevivió todo el período de la Edad Media.
Ptolomeo catalogó muchas estrellas, asignándoles un brillo y magnitud, ademas estableció normas para predecir los eclipses.
Su aportación fundamental fue su modelo del Universo: creía que la Tierra estaba inmóvil y ocupaba el centro del Universo, y que el Sol, la Luna, los planetas y las estrellas, giraban a su alrededor.
Aplicó sus estudios de trigonometría a la construcción de astrolabios y relojes de sol. Y también aplicó el estudio de la astronomía al de la astrología, creando los horóscopos. Todas estas teorías y estudios están escritos en su obra Tetrabiblon.

Aquí os dejo algún nombre más de matemáticos relevantes en la historia por si tenéis más curiosidad:

Anaximandro de Mileto

Filolao de Tarento

Aristarco de Samos

Eratósteles de Cirene

Clase 4 de diciembre de 2015

Querido diario:
comenzaremos hablando sobre LAS RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ALGUNOS ÁNGULOS.

Ángulos complementarios (a, 90°- a)

 

Ángulos suplementarios (a, 180° - a)

  

Ángulos que difieren en 180° (a , 180° + a)

  

Ángulos opuestos (a, -a) o que suman 360° (a , 360° - a)

                         

TEOREMA DEL SENO

En un triángulo cualquiera los lados son proporcionales a los senos de sus ángulos opuesto. 

    

Demostración:

primero trazamos la altura del triángulo para dividirlo en dos triángulos rectángulos.  

 

sen A = h/b ,  h= b * sen A / sen B = h/a , h = a * sen B

Igualamos las h y obtenemos : b * sen A = a * sen B

Despejamos y ya tenemos el teorema del seno:  a / sen A = b / sen B

TEOREMA DEL COSENO

En un triángulo cualquiera, el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de ellos por el coseno del ángulo que forman.

Demostración: