comenzaremos hablando sobre LAS RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ALGUNOS ÁNGULOS.
Ángulos complementarios (a, 90°- a)
Ángulos suplementarios (a, 180° - a)
Ángulos que difieren en 180° (a , 180° + a)
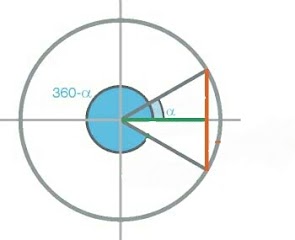
Ángulos opuestos (a, -a) o que suman 360° (a , 360° - a)
TEOREMA DEL SENO
En un triángulo cualquiera los lados son proporcionales a los senos de sus ángulos opuesto.
Demostración:
primero trazamos la altura del triángulo para dividirlo en dos triángulos rectángulos.
sen A = h/b , h= b * sen A / sen B = h/a , h = a * sen B
Igualamos las h y obtenemos : b * sen A = a * sen B
Despejamos y ya tenemos el teorema del seno: a / sen A = b / sen B
TEOREMA DEL COSENO
En un triángulo cualquiera, el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de ellos por el coseno del ángulo que forman.

Demostración:








No hay comentarios:
Publicar un comentario